description logics
Description logics are a family of formal knowledge representation languages. Usually, their expressivity is between propositional logic and first order logic.
Description Logics
Syntax
Below, we define the \(\mathcal{SROIQ}\) syntax.
RBox
RBox contains the roles axioms, roles are either the universal role or a role name \(r\) or its inverse \(r^{-}\).
The axioms are of the for \(r_{1} \circ r_{2} \circ \dots \circ r_{n} \sqsubseteq r\), si n > 1 it is called a transitivity statement.
TBox
Here, we list the possible concept expressions with \(C\) and \(D\) two concept expressions and \(r\) is a simple role:
- top, bottom
- nominal concepts, defined as finite set of individual name,
- negation or complementary, if \(C\) is a concept expression, then \(\neg C\) is a concept expression too,
- intersection, \(C \sqcap D\) is a concept expression,
- union, \(C \sqcup D\) is a concept expression,
- existential quantification, \(\exists r.C\) is a concept expression,
- universal quantification, \(\forall r.C\) is a concept expression,
- self restriction, if r is simple, \(\exists r.Self\) is a concept expression,
- at-least restriction, for \(n\) a natural number, \(\geq n r.C\) is a concept expression,
at-most restriction, for \(n\) a natural number, \(\leq n r.C\) is a concept expression,
Axioms are in a TBox are concept expressions inclusions, like \(C \sqsubseteq D\).
AL-languages
\(\mathcal{AL}\) is an abbreviation for attributive language. It allows the following concept descriptions:
- atomic concepts, top and bottom
- negation of atomic concept
- intersection
- universal quantification
limited existential quantification of the form \(\exists r. \top\)
The AL language can be extended with union (\(\mathcal U\)), full existential quantification (\(\mathcal E\)), at-least and at-most restriction (\(\mathcal N\)) and negation (\(\mathcal C\)).
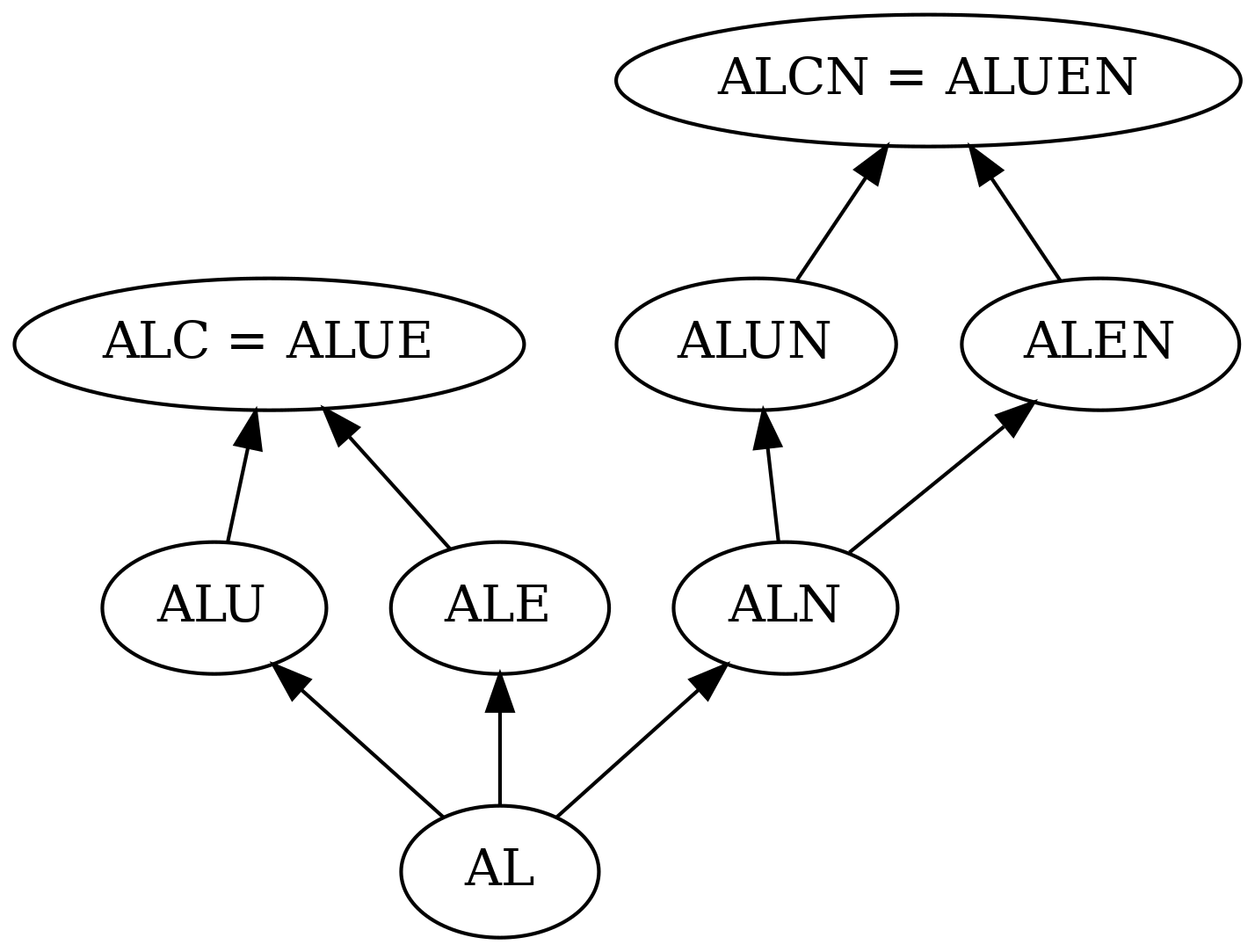
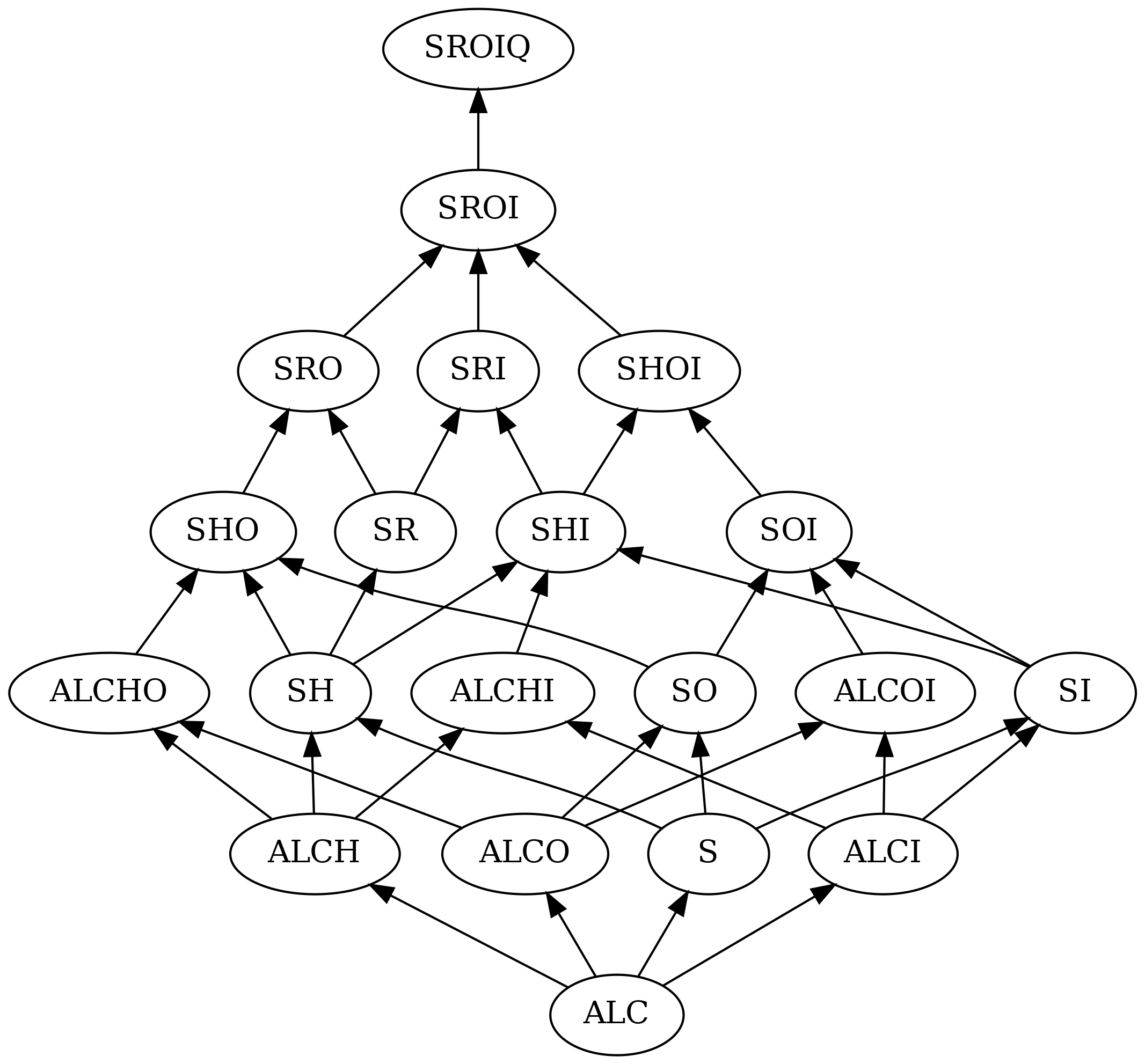
The letters S, R, O, I, F, N, Q
The letters:
- \(\mathcal S\) denotes \(\mathcal{ALC}\), where we additionally allow transitivity statements,
- \(\mathcal H\) in the name of a DL indicates that role hierarchy are supported,
- \(\mathcal SR\) denotes \(\mathcal{ALC}\) with all kinds of RBox axioms as well as self concepts,
- \(\mathcal O\) in the name of a DL indicates that nominal concepts are supported,
- \(\mathcal I\) in the name of a DL indicates that inverse roles are supported,
- \(\mathcal F\) in the name of a DL indicates that role functionally statements are supported (\(\perp \sqsubseteq \leq1 r.\top\)),
- \(\mathcal N\) in the name of a DL indicates that unqualified at-least or at-most restrictions are supported, i.e. \(\leq n r.\top\) or \(\geq n r.\top\),
- \(\mathcal Q\) in the name of a DL indicates that qualified number restrictions are supported.
The description logic EL
EL allows only concepts (no roles), which can be either the top concept, an atomic concept, the intersection of two concepts or the existential quantification of a concept (atomic or not). The TBox is a finite set of concept inclusions.
Metamodeling
OWL-Full
In DBLP:journals/logcom/Motik07, OWL-Full is represented as the most expressive of the Semantic Web ontology languages. Contrary to OWL-DL, OWL-Full does not impose the following restrictions:
- the sets of logical and metalogical symbols (e.g. rdf:type) are strictly separated,
- the sets of symbols used as concepts, roles and individuals are strictly separated,
restrictions required to yield a decidable logic, such as the one on simple roles in number restrictions.
Since 3. is not enforced in OWL-Full, OWL-Full is undecidable. The subset ALC-Full is undecidable if 1. and 2. are not enforced.
Systems
Reasoners
Knowledge base systems
- RDFox is C++ in memory RDF triple store. It supports RDFS, datalog and OWL2 RL reasoning and SPARQL queries.
Editors
- Protégé is a free, open-source ontology editor,
- WebVOWL is a web visualizer for OWL file
People
- Uli Sattler gives a talk about the description logics reasoners at KR 2021