existential rules

Existential rules are first order logic formulas mainly used for knowledge representation.

Query answering problem

The general problem of query answering over an instance with a set of existential rules is undecidable DBLP:journals/jair/CaliGK13.

Deciding the query answering problem

There are known three classes of rules for which the problem of conjunctive query answering is decidable.

see: DBLP:phd/hal/Thomazo13

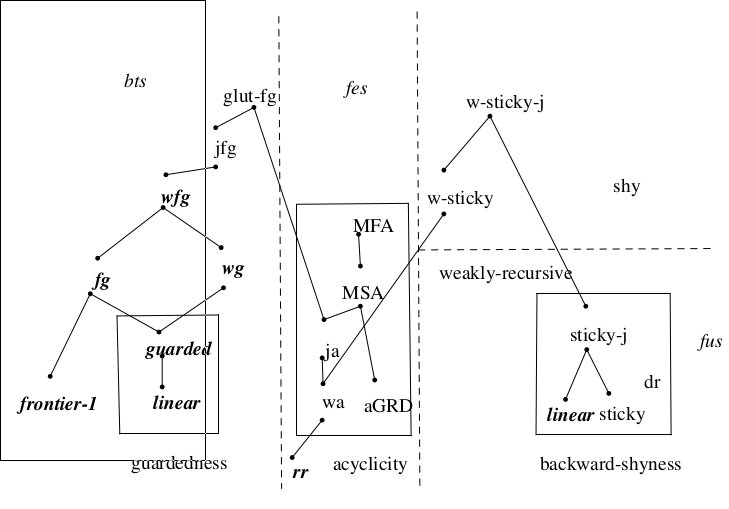
2021-07-26_09-44-40_screenshot.png

Finite expansion set (fes)

In this case, there always exists an finite canonical model of any facts and the rules we consider, which can be computed using the core chase and on which we can evaluate the query to get the answers.

The FES property is undecidable for general existential rules.

For the guarded fragment, we know that the termination of the oblivious and the semi-oblivious chase is decidable grecoChaseTerminationConstraints2010, which is not sufficient to obtain the decidability of the FES property.

Bounded treewidth set (bts)

In this case, the rules are such that from any facts, there exists a bound such that any derived facts using the core chase have a treewidth lower than this bound.

Finite unification set (fus)

In this case, there is a first-order rewriting of any conjunctive query w.r.t. the rules. It is equivalent to say that for any conjunctive query \(q\), there exists a union of conjunctive query, which is a rewriting of \(q\) w.r.t. the rules. It is also equivalent to say that the rules satisfy the bounded derivation-depth property meaning that for any query there exists an bound on the chase steps such that the query answers can be found using this bounded chase on any fact.

The following rule is 1-frontier, datalog and guarded, but do not form a fus: \(R = A(x), T(x, y) \rightarrow A(y)\). For example, consider the query \(q() \leftarrow A(x), B(x)\) and the fact \(F_{n} = A(c_{0}), T(c_{0}, c_{1}), \dots, T(c_{n-1}, c_{n}), B(c_{n})\). It shows that the rule set \(\{ R \}\) does not satisfy the bounded derivation-depth property.

Fontier-guarded rules FUS property is decidable DBLP:conf/ijcai/BarceloBLP18.

A Datalog rule set is FUS if and only if it is bounded DBLP:journals/jcss/AjtaiG94.

An algorithm of query rewriting with rules have been presented in the thesis of Mélanie König: DBLP:phd/hal/Konig14.

Chase

The importance of the chase in many applications is due to the fact that several problems can be solved by exhibiting a universal model, and the chase computes a universal model, when it terminates DeutschChaseRevisited2008. An universal model is a model that can be mapped to any model or that is more general than any model. The certain answer of a query be computed by evaluated it on the universal model, instead of on every model.

Chase variants

  • oblivious chase (obl): for each h morphism from B to D, then we add hsafe(H) to the KB,
  • semi-oblivious chase or Skolem chase (sobl): for each h morphism from B to D, then we add hsafe(hf)(H) to the KB, where the safe operation only depends of hf: the value of h on the frontier variables,
  • restricted chase or standard chase (std): for each h morphism from B to KB, then we add hsafe(H) to the KB to form KB', if h can not be extended to map H to the KB.
  • core chase (core):

Chase termination classes

With TGDs only, the chase can either terminate or run forever.

As explained in DBLP:journals/pvldb/CalauttiGMT16, we have the following classes \(CT^{c}_{\forall}\) (resp. \(CT^{c}_{\exists}\)) of sets of TGDs \(\Sigma\) such that the chase terminates on all every database, on every (resp. at least on one) c chase executions.

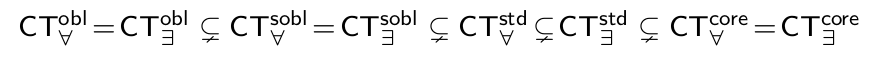
2021-06-16_13-01-26_screenshot.png

Example of TGD set where there exists a std chase executions that terminates and some that doesn't:

  1. \(E(x,y) \rightarrow E(x,z)\)
  2. \(E(x,y) \rightarrow E(y,y)\)

Example of TGD set where the core chase terminates, but the std chase doesn't, consider \(p(x,x), p(x,y) \rightarrow p(y,y), p(y,z)\) on \(\{p(a,a), p(a,b) \}\).

Boundedness

For the oblivious chase:

  • undecidable for datalog in general
  • decidable for guarded frontier
  • ? for frontier guarded

Piecefulness

System

Resources

This post accepts webmentions. Do you have the URL to your post?

Otherwise, send your comment on my service.

Or interact from the fediverse with your username:

fediverse logo Share on the Fediverse